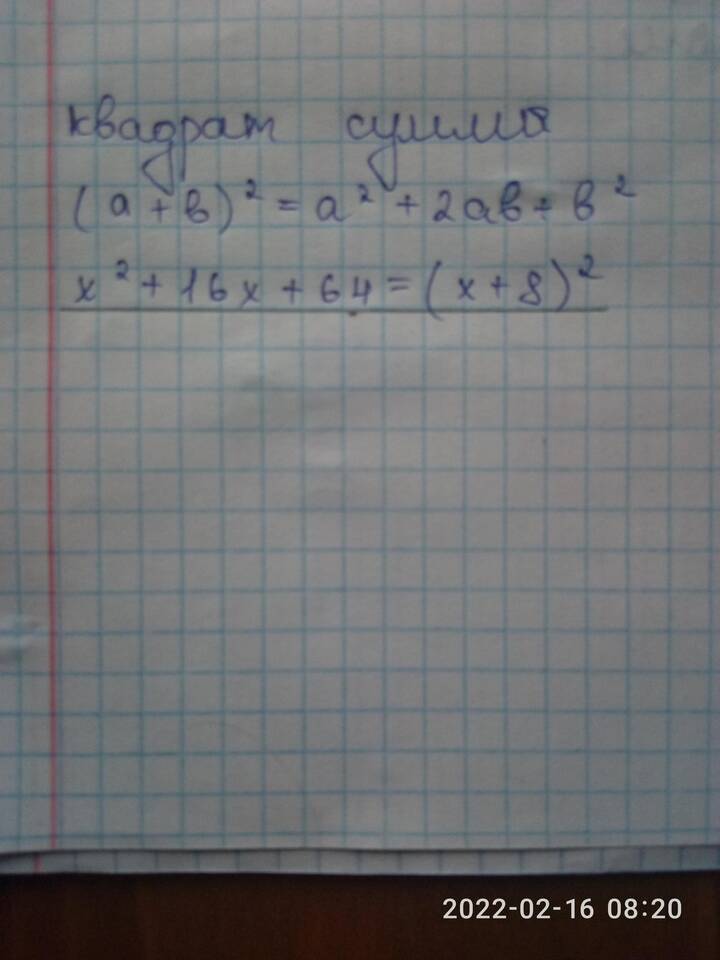Представление математических выражений в виде суммы является важным навыком в алгебре и анализе. Рассмотрим основные методы разложения выражений на слагаемые.
Содержание
Основные методы представления в виде суммы
- Разложение многочленов
- Разложение дробей на простейшие
- Тригонометрические преобразования
- Биномиальное разложение
- Разложение в ряды
Разложение многочленов
Примеры разложения
| Исходное выражение | Представление в виде суммы |
| (x+2)(x+3) | x² + 5x + 6 |
| 2x³ - 4x² + x | 2x³ + (-4x²) + x |
Разложение дробей
- Определить знаменатель и его корни
- Записать предполагаемую форму разложения
- Найти неизвестные коэффициенты
- Записать окончательное разложение
Пример:
(3x+5)/(x²-1) = A/(x-1) + B/(x+1)
Тригонометрические преобразования
- sin(a+b) = sin a cos b + cos a sin b
- cos 2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
- tg(x+y) = (tg x + tg y)/(1 - tg x tg y)
Биномиальное разложение
| Формула | Пример |
| (a+b)² = a² + 2ab + b² | (x+3)² = x² + 6x + 9 |
| (a-b)³ = a³ - 3a²b + 3ab² - b³ | (2x-1)³ = 8x³ - 12x² + 6x - 1 |
Разложение в ряды
- Ряд Тейлора: f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ...
- Ряд Фурье: f(x) = a₀/2 + Σ(aₙcos(nx) + bₙsin(nx))
- Биномиальный ряд: (1+x)ᵐ = 1 + mx + m(m-1)x²/2! + ...
Практические рекомендации
При представлении выражений в виде суммы важно соблюдать правила алгебраических преобразований и проверять эквивалентность исходного и преобразованного выражений. Для сложных случаев используйте математические пакеты (Wolfram Alpha, Maple, Mathcad).